Los huesos lisos de Sharma incisos por rastros irregulares que se originan en 20,000 años de arqueólogos confundidos hasta que notaron algo único: líneas ethómicas como Tally Marx, pueden haber sido los principales números. Del mismo modo, una tableta de arcilla de 1800. a. C. ingresada por los números de Babilonia describe el sistema del sistema basado en los números principales.
Al igual que Ishango Kost, tabletas Plympton 322 y otros artefactos a lo largo de la historia, los principales números fascinaban y encantaban a las personas durante la historia. Hoy, los números reales y sus propiedades se estudiaron en la teoría del número, una rama de las matemáticas y un área activa de investigación hoy.
Historia de números importantes

Algunos científicos especulan que las etiquetas en los huesos de Ishango representan los principales números. Joeikentin / Vikimedia Commons, CC BI-SA
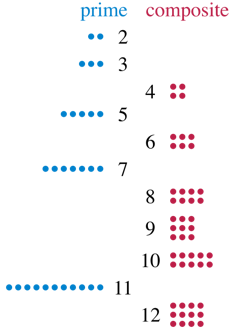
Informal, se observó un número positivo de recuentos mayores que uno si ese número de puntos solo se puede organizar en una cadena rectangular con una columna o un turno. Por ejemplo, 11 es el número principal de 11 puntos de forma solo secuencias rectangulares 1 a 11 y 11 a 1. Contraste, 12 no es un primer ministro porque puede usar un rango de 3 a 4 puntos, con múltiples filas y más columnas. Los libros de texto matemáticos definen el número principal como un número entero que excede a aquellos cuyas únicas partes positivas son solo 1 y ella misma.
Historian Mathematics Peter S. Rudman sugiere que el matemático griego probablemente entendió el concepto de números importantes, alrededor de 500 a. C.
Alrededor de 300 a. C., el matemático griego y la lógica Euruler mostraron que hay infinitos números principales. Euler comenzó a asumir que hay un número de aplicación final. Luego se le ocurrió al primer ministro que no estaba en la lista original para crear contradicción. Dado que el principio básico de las matemáticas está lógicamente en línea sin contradicciones, y Euler concluyó que su suposición original debe ser falsa. Entonces, hay una gran aplicación interminable.
El argumento ha establecido la existencia de una aplicación infinitamente mucha, pero no fue particularmente constructiva. Euler no tenía un método efectivo para indicar todas las promesas en la lista actualizada.
Los números extensos, cuando se expresan como ese número de puntos, solo se pueden organizar en una línea o columna, no en un cuadrado o rectángulo. David Eppstein / Vikimedia Commons
En la Edad Media, el matemático árabe progresó a los griegos de la teoría de los números principales, llamado números de Hasam en ese momento. El matemático persa, Kamal al-Din al-Farisi, formuló el teorema básico de la aritmética, quien dice que cualquier entero positivo mayor que uno puede expresarse de manera única como un producto.
Desde este punto de vista, los principales números son los bloques de construcción básicos para la construcción de cualquier entero positivo utilizando multiplicación, similar a los átomos que se combinan para hacer moléculas en química en química.
Los números de aplicación se pueden clasificar en diferentes tipos. 1202. Año, Leonardo Fibonactions presentó "Liber Acis: Libro de cálculo" Aplicar números de formulario (2p - 1) donde también se recibe.
Hoy, Mersenne Primescu después del monje francés Marin Mersenne se llama de esta forma de esta forma. Muchas de las aplicaciones bien conocidas más grandes siguen este formato.
Varios matemáticos tempranos creían que varias formas (2p - 1) estaban a cargo cada vez que P Primer Ministro. Pero en 1536. Año, el matemático Hudalricus Regius notó que 11 es el Primer Ministro, pero no (211 - 1), que es 2047. Años. El número 2047 se puede expresar como 11 veces 89, que es 11 veces 89.
Aunque no siempre es cierto, los teóricos de los números se han dado cuenta de que el atajo (2p - 1) a menudo produce recepción y ofrece una forma sistemática de buscar excelentes aplicaciones.
Buscar escenas grandes
El número (2p - 1) es mucho mayor en comparación con el valor de P y brinda oportunidades para reconocer grandes aplicaciones.
Cuando el número (2p - 1) se vuelve lo suficientemente grande, es mucho más difícil verificar si es (2p - 1) Premier, es decir, los puntos (2p - 1) solo se pueden organizar en una matriz rectangular con una columna o una línea.
Afortunadamente, Edouard Lucas fue 1878. Desarrollé una prueba del problema principal en 1878. Año, más tarde demostró a Derrick Henry Lehmer 1930. Su trabajo ha resultado en un algoritmo eficiente para evaluar posibles aplicaciones de yeñales. Usando este algoritmo con cálculos manuales en papel, Lucas mostró 1876. Año de que un número de 39 dígitos (2127 - 1) es de 170,141,183,460,469,231,731,687,303,715,884,105,727, y ese valor es el primer nivel.
También se conoce como el M127, este número sigue siendo el mejor mejor verificado por composiciones manuales. Mantuvo un récord para el mejor primer ministro conocido 75 años.
Los investigadores comenzaron a usar computadoras en la década de 1950 y el ritmo de detectar nuevas aplicaciones grandes. En 1952. Raphael M. Robinson identificó cinco nuevas aplicaciones marsenniales utilizando una computadora automática estándar de Westerner para realizar la prueba de ejemplo de Mucas-Lehmer.
A medida que las computadoras han mejorado, se convirtió en la lista de primos de Mersenna, especialmente con la llegada de Crai Cupin 1964. Aunque hay aplicaciones infinitas, los investigadores no están seguros de cuántos tipos (2p - 1) y Mersenne se reciben.
Hasta principios de la década de 1980, los investigadores acumularon suficientes datos para creer con confianza que el Príncipe Mersennene es infinito. Incluso podrían adivinar con qué frecuencia estos números principales aparecen en promedio. Los matemáticos hasta ahora no han encontrado evidencia, pero los nuevos datos continúan respaldando estas conjeturas.
George Voltman, informático, fundó Great Internet Mersenne Prime, o Gimps, 1996. Años. A través de este programa de colaboración, todos pueden descargar libremente el software gratuito disponible desde el sitio web de Gimps para buscar Merennene Bugs en sus computadoras personales. El sitio contiene instrucciones especiales sobre cómo participar.
Gimps ahora ha identificado 18 aplicaciones de Mersenne, principalmente en computadoras personales utilizando chips Intel. El programa ha sido instalado por un promedio de un nuevo descubrimiento sobre cada uno o dos años.
El primer primer ministro famoso
Luka Durant, programadora retirada, descubrió el récord actual para el primer ministro más grande conocido, (2136.279.841 - 1), en octubre de 2024. años.
Se llama M136279841, este número de 41.024.320 dígitos se identificó 52. Mersenne Prime y se encontró ejecutando GIMP en una red informática basada en la nube disponible públicamente.
Esta red fue utilizada por Nvidia Chips y asumió 17 países y 24 centros de datos. Estos chips avanzados proporcionan una computación más rápida al manejar miles de presupuestos al mismo tiempo. El resultado es un tiempo de ejecución más corto para algoritmos como probar los números principales.

Los nuevos y cada vez más fuertes chips de computadora han permitido que los cazadores de campeonatos se conviertan en ejemplos cada vez mayores. Fritzchens Fritz / Flickr
Frontier Electronic Foundation es un grupo civil Libertie que ofrece premios en efectivo para identificar grandes. Recibieron premios en 2000. Y 2009. Año por el primer dígito verificado por primera vez y 10 millones de números principales de dígitos.
Dos desafíos presentados de grandes números importantes son identificar los primeros 100 millones de dígitos y mil millones y entumecimiento y 1 mil millones y numblas y 1 mil millones de aplicaciones. Premios EFF de 150,000 y 250,000 USD, es decir, esperan el primer individuo o grupo exitoso.
Ocho 10 primeros ministros famosos más grandes son Mersenna, por lo que Gimps y Clocuming Computing están listos para desempeñar un papel destacado en la búsqueda de un delito menor récord con grandes números de capital.
Los grandes números principales juegan un papel vital en muchos métodos de cifrado de seguridad de cibre, por lo que cada usuario de Internet se beneficia de las búsquedas de grandes números principales. Estas búsquedas ayudan a mantener comunicaciones digitales e información confidencial.

0 Comentarios