Considere las matemáticas y con más precisión en una clase matemática: ¿ha considerado las operaciones, la fórmula y el ejercicio? Es común. Sin embargo, tienen mucho más que ver con el razonamiento, la comunicación, la resolución de problemas, la representación. Poner un enfoque en la clase en ambos lados afecta las emociones, el tamaño autosuficiente (si creemos que les dan buenas o malas) y la creencia de los estudiantes hacia las matemáticas.
Investigamos estas tres dimensiones (emociones, complacencia y creencias) cuando continúan las matemáticas para tener un enfoque "instrumental" (basado en reglas y procedimientos sin significado) a "relacional" (basado en una comprensión profunda del contenido). Y demostramos que permite a los estudiantes vivir un objeto de una manera más positiva para sentirse competente en matemáticas y construir una visión rica de lo que significa hacer.
Si es mejor objetivo, ¿por qué es tan difícil adoptar este modelo en una clase matemática? Continuar el plan de estudios, la orientación internacional y la literatura científica afectan su importancia, pero los maestros a menudo vuelven a realizar modelos de enseñanza similares a aquellos que tienen experiencia como estudiante, y los libros de texto generalmente favorecen este enfoque.
Punto de partida instrumental
Es suficiente ver los libros de texto habituales para confirmar que la enseñanza de las matemáticas, tanto en la escuela primaria como en la secundaria, todavía está marcada por un enfoque instrumental: "Está hecho, el ejercicio, se repite".
Esto es exactamente lo que es cuando analizamos la descripción de un grupo de 19 estudiantes al comienzo del cuarto grado: las matemáticas más comunes como tema centrada en la cirugía. "Los problemas son plural, sumas, confiscación ...", escribió un estudiante.
En estos escritos, los estudiantes aplicaron su competencia en matemáticas como bajas. Las emociones, cuando son positivas, se limitaron a "como" sin más profundidad. El mensaje fue claro: las matemáticas fueron ejercicios aritméticos de rutina que tuvieron que superarse. Las referencias no se hacen para explicación y comprensión.
Gire hacia la resolución de problemas
En un modelo instrumental de educación, se fomenta una comprensión superficial del contenido, porque su aprendizaje requiere un recuerdo de una serie de reglas. ¿Quién nunca escuchó la frase "No tienes que entender ahora, solo hazlo"? Incluso en películas como Memory ayer (1991) aparece esta tendencia.
Las tareas realizadas suelen ser rutinarias, ejercicios, mientras que los problemas a menudo reducen los ejercicios con un contexto que actúa como decorado, sin contribuciones. Es posible que en este modelo, los verdaderos problemas ocurran al final, asumir un desafío y para el cual no existe una regla de resolución directa.
A Lire Aussi: ¿Por qué son los problemas con el rollo de matemáticas (y cómo evitarlo)
En contraste, una comprensión profunda del contenido se realiza en el modelo relacional. El objetivo ya no es aprender una variedad de reglas sin significado, sino para conectar la experiencia previa para construir nuevos conocimientos.
Es necesario movilizar procesos que indiquen actividad matemática de calidad: resolución de problemas; razonamiento, asunción y evidencia; argumentación; Comunicación; representación; Enlaces dentro y fuera de las matemáticas. Aprender a través de la resolución de problemas significa que los estudiantes enfrentan problemas auténticos y cuidadosamente seleccionados, sin recibir la instrucción anterior que los convierte en ejercicios. Está en la resolución de estos problemas, con el andamio adecuado del maestro (normalmente en forma de preguntas), donde aparece un nuevo contenido.
Por ejemplo, calcular el área "inclinada" en la red es un problema. Si no se conoce el teorema de Pitágoras, por supuesto:
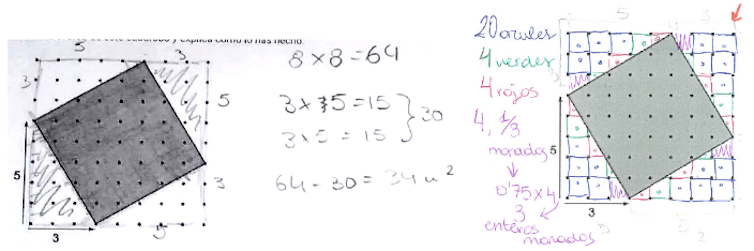
En la imagen, podemos ver dos técnicas que los estudiantes insertan en el juego para resolverlo. Este problema crea una extensión directa, porque si se propone explorar el área cuadrada con diferentes "preferencias", la generalización lo coloca en un teorema de bandeja conocido. Tenga en cuenta que si el teorema se proporciona por primera vez, como se haría en el modelo instrumental, el problema se convierte en un ejercicio de rutina.
Trabajar con un enfoque relacional
A lo largo del curso, nuestro grupo de 19 estudiantes trabajó en la resolución de problemas y metodología, como aulas en el habla, conocido en español como aulas para pensar, creado por el libro adjunto, profesor sueco, profesor sueco, Peter Liljedahl. Este trabajo incluye una serie de técnicas que facilitan la creación de la cultura en el aula destinada a resolver problemas. Por ejemplo, para que los estudiantes los enfrenten, en tablones verticales para eliminar y grupos aleatorios de tres. De esta manera, la interacción se multiplica, al mismo tiempo que el maestro se vuelve más consciente de lo que hacen los estudiantes.
El cambio fue radical. En junio, 15 de los 19 estudiantes discutieron las matemáticas como algo que tenía que ver con comprender, pensar, trabajar en un grupo y encontrar sentido. Ya no era una cuenta, sino también procesos. La niña resumió su experiencia:
"Las matemáticas para mí es que puedo entender los números. Me gusta trabajar en grupos en placas negras en lugar de hacerlo solo".
Este cambio de enfoque no solo ha convertido una visión del sujeto. La autolesión de la competencia también se ha incrementado: seis estudiantes ahora se sienten "bien en matemáticas", frente a solo uno al principio. Y en el plano emocional, 16 de 19 expresaron entusiasmo, entretenimiento y serenidad, conectando sus emociones positivas con actividades específicas como resolver problemas difíciles o cooperación en grupos.
El aula dejó de ser un lugar donde los procedimientos se repiten para convertirse en espacio para la investigación y el descubrimiento conjunto.
Volver al modelo de exhibición
La historia, sin embargo, no termina allí. En enero del próximo curso, pero en 5. Grado, los mismos estudiantes volvieron al acceso instrumental, basado en ejercicios individuales y clases de exhibición. Reenviamos los escritos al comienzo del curso en el que compartieron sus emociones y creencias sobre este tema. El contraste fue un momento. Menos de la mitad de la escritura ahora incluía una visión clara de las matemáticas, y muchos reflejaron aburrimiento o desalentador, como significa un estudiante:
"Este año, los amigos son aburridos porque la mayoría de las veces hacen cuentas".
Es interesante que la percepción de la competencia siga siendo alta: doce estudiantes se sintieron seguros. Pero las emociones se volvieron negativas para aquellos que disfrutaron del aprendizaje relacional. Una incoja entre lo que eran antes de vivir y lo que ahora se encontraron en la clase generó frustración.
Al mismo tiempo, el segundo grupo de estudiantes mostró alivio: "Casi no tenemos ningún problema difícil ... me encantan las matemáticas". Para algunos, la baja demanda cognitiva fue cómoda, aunque estimula un poco.
¿Qué son estos nos encuentran?
Los resultados de esta pequeña investigación confirman algo de que la literatura científica internacional se ha subrayado durante años: una cultura en las condiciones del aula de asistencia a los estudiantes con matemáticas. Un enfoque basado en la resolución de problemas no solo ofrece un aprendizaje significativo, sino que también promueve emociones positivas y aumenta la confianza en sus habilidades. Por el contrario, volver al modelo instrumental puede erosionar esta conexión, especialmente en aquellos que descubrieron que las matemáticas podrían ser más que una cuenta.
Este artículo se basa en la investigación en la que Manuel Jesús cooperó a Siaba-Lecton, un maestro de Ricardo Tobio, Esteiro-Muros Ceip (La Coruna).

0 Comentarios